
¿Qué es una vivienda?
¿Qué es una vivienda?
La vivienda es una de las necesidades materiales más esenciales de la humanidad. Abarca multiples dimensiones y por lo tanto puede ser analizada desde diferentes visiones. Desde una visión sociológica, además de representar un refugio, tambien contiene atributos subjetivos como estatus e identidad social, lo que motiva la agrupación espacial de individuos con caracteristicas semejantes y a su vez refleja la división de la estructura social. Estas aglomeraciones muestran y definen el lugar de cada individuo dentro de la ciudad y revelan la forma diferenciada de acceso y apropiación de los recursos urbanos. Se suele argumentar que el lugar de residencia de la población determina, en gran magnitud, las oportunidades a las que tiene acceso (Garrido Rodríguez et al., 2023).
Desde la economia espacial la vivienda, como mercancía, es única de multiples formas y comparte ciertos aspectos de la visión sociológica. Es durable y, gracias a la necesidad de suelo para su producción, espacialmente inmóvil. Su localización implica efectos relacionados con el vecindario en terminos de externalidades positivas y negativas, y con la accesibilidad a los centro de empleo, lo que significa que su posición relativa y el entorno urbano son fundamentales en la conformación del valor. Es decir, las familias no solo compran los atributos estructurales del inmueble, sino también una variedad de servicios en una ubicación particular (Kain y Quingley, 1975; Wilkinson, 1973). Esto convierte a la vivienda en un bien complejo cuya percepción de valor no solo proviene de sus atributos internos sino de la conjunción con los atributos externos.
Existen viviendas de distinto tamaño, edad, calidad, estilo, amenidades, vecindarios y localizaciones. La heterogeneidad sumada a la oferta relativamente inelastica, resulta en una tendencia natural a la segmentación en diferentes submercados, en función de sus características estructurales, patrones de accesibilidad y características de la población que las habita (Straszheim, 1975).
Tiene un precio alto, por lo que su demanda también depende de la disponibilidad de crédito y financiamiento. Mudarse es costoso no solo en términos monetarios, por lo tanto, cuando el ingreso o las preferencias cambian, los consumidores no ajustan instantáneamente su consumo de vivienda. Y su producción está relacionada con el crecimiento económico (Bluestone et al., 2008; Sobrino, 2014).
Estas particularidades caracterizan el funcionamiento del mercado residencial. Su reconocimiento, y el de las complejidades que involucran, condujo al desarrollo de diferentes cuerpos teóricos para explicar la racionalidad, bajo principios económicos, de la conformación de los precios y las dinámicas espaciales del mercado de vivienda (Bluestone et al., 2008).
 Unequal Scenes, Johnny Miller
Unequal Scenes, Johnny Miller
 Acceso a la ciudad
Acceso a la ciudad
 Heterogeneidad
Heterogeneidad

¿Cómo se analiza su precio?
¿Cómo se analiza su precio?
En el mercado de vivienda, como en otros mercados, la interacción entre oferta y demanda es fundamental en la determinación de los precios, los cuales actúan como mecanismo de asignación de las viviendas entre los consumidores, de acuerdo con sus ingresos y restricciones presupuestarias (Kirby, 1976). La descripción de este equilibrio suele plantearse en términos de la teoría del consumidor; sin embargo, en el caso de la vivienda, la necesidad de suelo y la heterogeneidad espacial hacen que no sea posible simplemente agregar las demandas individuales en una demanda de mercado homogénea, pues esta depende de las características específicas de cada localización.
Por tal motivo se han desarrollado distintos ajustes a los conceptos tradicionales usados para formular el equilibrio de mercado con la intención de considerar las características particulares de la vivienda y usar la racionalidad económica para explicar sus procesos y productos. Estos ajustes han sido materializados en dos perspectivas analíticas fundamentales.
Modelo de localización
La primera y más antigua es el modelo clásico de localizacion que se desarrolló a partir del trabajo de Von Thunen (1826); estableció, para el caso agrícola, que la renta de un predio se determina por el excedente económico que puede brindar una localización, el cual es determinado por la diferencia entre los ingresos y los costos totales, que incluyen a los costos de transporte (Alonso, 1964). Supone que los agentes son idénticos en el sentido de que producen la misma cantidad de productos con los mismos costos, pero difieren en su localización. Por lo tanto, aquellos localizados cerca del mercado central tienen un mayor excedente económico debido a los bajos costos de transporte. Al alejarse del centro, los costos de transporte aumentan y, por lo tanto, el excedente económico disminuye. Este proceso es conocido como el principio residual, siendo que el monto de renta es el residuo después de pagar los costos de producción, los costos de transporte y la ganancia media de la actividad (Garrido Rodríguez et al., 2023).
Este mecanismo fue adaptado al entorno urbano en donde no existe solo un tipo de usuario, sino distintos tipos, con actividades diferentes, que compiten por acceder al mercado central, también conocido como Distrito Central de Negocios (DCN). Los agentes no solo valoran los costos de transporte, sino que también la accesibilidad y las economías de aglomeración que brinda el DCN. En el caso del sector residencial, el factor locacional clave son los costos de traslado, es decir, el costo de los viajes que realiza la población para llegar a su lugar de trabajo.
El terrateniente busca maximizar sus ganancias, por lo que las distintas curvas de demanda de los potenciales usuarios se comparan en todas las localizaciones y en cada una el suelo se asigna al mayor postor. La superposición de estas disposiciones a pagar genera una curva envolvente de renta (Gráfica 1), donde en cada ubicación prevalece el uso más productivo (residencial, comercial o industrial), definiendo el patrón espacial de la ciudad (Alonso, 1964). Esta curva representa el equilibrio locacional y se alcanza cuando los costos y beneficios de cambiar de ubicación se igualan, garantizando que todos los agentes obtengan el mismo nivel de satisfacción, independientemente de su localización (Mills y Hamilton, 1984).
Un obstáculo mayor de esta perspectiva analítica es la heterogeneidad en la vivienda (Witte et al., 1979). El modelo supone que las preferencias de los consumidores son iguales y, por tanto, supone una vivienda homogénea en términos de calidad. El reconocimiento de esta y otras limitaciones provocó una transición en la literatura internacional de las teorías de localización a nuevas aproximaciones metodológicas para analizar el mercado de vivienda en las ciudades modernas. Para considerar la inherente heterogeneidad de la vivienda, muchos análisis recientes han visto la vivienda en términos hedónicos o de atributos.
Modelo hedónico
La segunda perspectiva de análisis del mercado de vivienda constituye una aproximación que introduce las complejidades asociadas a la heterogeneidad del bien. El modelo fue desarrollado por Rosen, (1974) a partir de los avances de Lancaster (1966), sobre la teoría del consumidor. Su principal innovación consiste en romper con la visión tradicional de que los bienes son objetos directos de utilidad y establece que son las propiedades de los atributos del bien de donde surge la utilidad (Lancaster, 1966). De tal forma, el modelo de Rosen descompone a la vivienda en un conjunto de características, cada una de los cuales ofrece un flujo particular de servicios al residente (Griliches, 2013; Richardson et al., 1974; Rosen, 1974). El objetivo del modelo es describir el equilibrio competitivo en un mercado de bienes heterogéneos en el que vendedores y compradores interactúan (Rosen, 1974; Taylor, 2008).
La vivienda se introduce como un bien diferenciado, descrito por un vector de atributos 𝑉=( 𝑣1,𝑣2,…𝑣𝑛). Cada vivienda tiene un precio de mercado observado asociado a un conjunto particular de valores del vector V, lo que permite revelar implícitamente una función de precios 𝑃𝑖 = 𝑃(𝑣𝑖1,𝑣𝑖2,…𝑣𝑖𝑛). La derivada parcial de P(.) respecto a la característica vj, 𝜕𝑃/𝜕𝑣𝑗, representa el precio marginal implícito de dicha característica, manteniendo las demás constantes (Brown y Rosen, 1982; Greenstone, 2017; Rosen, 1974).
El equilibrio competitivo se fundamenta en las decisiones de compradores y vendedores quienes, bajo los supuestos de competencia perfecta e información completa, maximizan su utilidad o beneficios, sujetos a las restricciones de su ingreso y del mercado. Para los consumidores, la utilidad depende de dos elementos: el consumo de un bien compuesto, X, que representa todos los demás bienes (comida, ropa, transporte, ocio); y el conjunto de atributos que integran la vivienda, V. Así, su función de utilidad se define como:
\[ U = U(X, V) \]
Si se asume que el consumidor solo compra una vivienda, entonces la restricción presupuestaria se expresa como I=P+X, donde I es el ingreso. Sustituyendo la restricción presupuestaria en la función de utilidad resulta en:
\[ U = U \big( I - P, \, v_1, v_2, \dots, v_n \big) \]
Para analizar la demanda respecto a un atributo particular, se invierte la función de utilidad, manteniendo constantes todas las características salvo vj. Esto permite derivar la disposición marginal a pagar por ese atributo:
\[ D_j = D_j \big( I - P, \, v_j ; \, V_{-j}^*, \, u^* \big) \]
Aquí, u* es el máximo nivel de utilidad alcanzable dado el ingreso y V*-j es el vector óptimo de atributos, excluyendo la característica vj. Esta función representa la curva de demanda o de indiferencia, ya que muestra la cantidad máxima que un individuo está dispuesto a pagar por diferentes cantidades de vj, manteniendo la utilidad constante (Greenstone, 2017; Taylor, 2008). El modelo es simétrico, por lo que del lado de la oferta la curva de oferta se construye de forma análoga.
La condición de equilibrio del consumidor se alcanza cundo se maximiza la utilidad sujeta a la restricción presupuestaria. Esta condición requiere que el consumidor elija una combinación óptima del bien compuesto X y de cada atributo de la vivienda vj, de manera que la tasa marginal de sustitución entre vj y X sea igual al precio marginal implícito del atributo vj. Matemáticamente, esto se expresa como:
\[ \frac{\tfrac{\partial U}{\partial v_j}}{\tfrac{\partial U}{\partial X}} = \frac{\partial P}{\partial v_j} \]
Esta igualdad representa una situación de equilibrio en la que el beneficio adicional de obtener una unidad extra del atributo vj, en relación con el bien numerario X, se iguala al costo adicional que impone el mercado por esa unidad extra, es decir, su precio marginal implícito. En este punto, el consumidor no tiene incentivos para modificar su elección, ya que cualquier cambio resultaría en una menor utilidad o mayor costo (Greenstone, 2017; Taylor, 2008).
En equilibrio, la interacción entre compradores y vendedores en el mercado de vivienda genera una coincidencia entre sus respectivas decisiones óptimas. Las funciones de demanda de los consumidores y de oferta de los productores se intersecan en un conjunto de puntos en los que ambos maximizan su utilidad o beneficios. Estas intersecciones comparten un gradiente comun que define la pendiente de la función de precios implícitos del mercado. Como resultado, las observaciones empíricas de precios de vivienda, Pi, conforman una envolvente conjunta de curvas de oferta y demanda individuales, reflejando las condiciones de tangencia que se presentan en cada punto de equilibrio (Gráfica 2) (Rosen, 1974; Taylor, 2008). Esta envolvente, que describe cómo varía el precio de mercado en función de los atributos del bien, recibe el nombre de Función de Precios Hedónicos (FPH).
La aplicación de la metodología hedónica se realiza mediante un proceso de dos etapas interrelacionadas. En la primera etapa, se estima la FPH o Pi mediante un análisis de regresión múltiple, utilizando datos transversales de los precios de venta de las viviendas y sus atributos (Griliches, 1971; Taylor, 2008). Esta etapa permite calcular los precios marginales implícitos de los atributos de la vivienda, los cuales revelan la disposición marginal a pagar por una unidad adicional de un atributo. En la segunda etapa se estima la demanda agregada por los atributos de la vivienda, utilizando los precios marginales implícitos obtenidos en la primera etapa e informacion sobre las caracteristicas de los consumidores. Sin embargo, la segunda etapa se considera un terreno fertil de problemas de identificación específicamente respecto a la distinción entre efectos de oferta y demanda.
Por tal motivo, la mayor parte de los estudios se concentran en la estimacion de la primera etapa, es decir de la Función de Precios Hedonicos (Taylor, 2008).
El modelo hedónico delimita un procedimiento para estimar la disposición a pagar de los individuos por bienes y servicios publicos lo que permite estimar relaciones de extraordinaria importancia para la determinación de una política óptima. Como se mencionó, la elección de vivienda, además de relacionarse con el consumo de las características estructurales, también se relaciona con las características locacionales resultado de las externalidades que enfrenta una ubicación particular. Por tanto, las elecciones observadas sobre vivienda revelan al investigador información sobre las preferencias subyacentes por estos elementos u otras características de interés (Taylor, 2008).
Ejemplos clásicos incluyen la calidad del medio ambiente, de las escuelas, de equipamientos e infraestructura urbana, así como de fenómenos sociales como el crimen y la segregación (Greenstone, 2017).
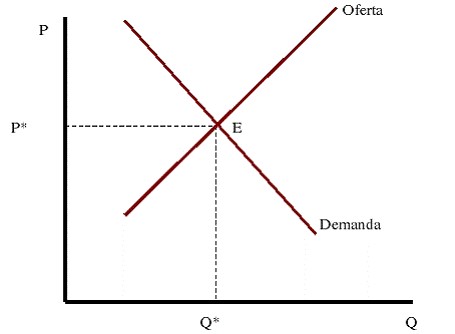 Equilibrio de mercado
Equilibrio de mercado
 Der isolierte Staat, (1826)
Der isolierte Staat, (1826)
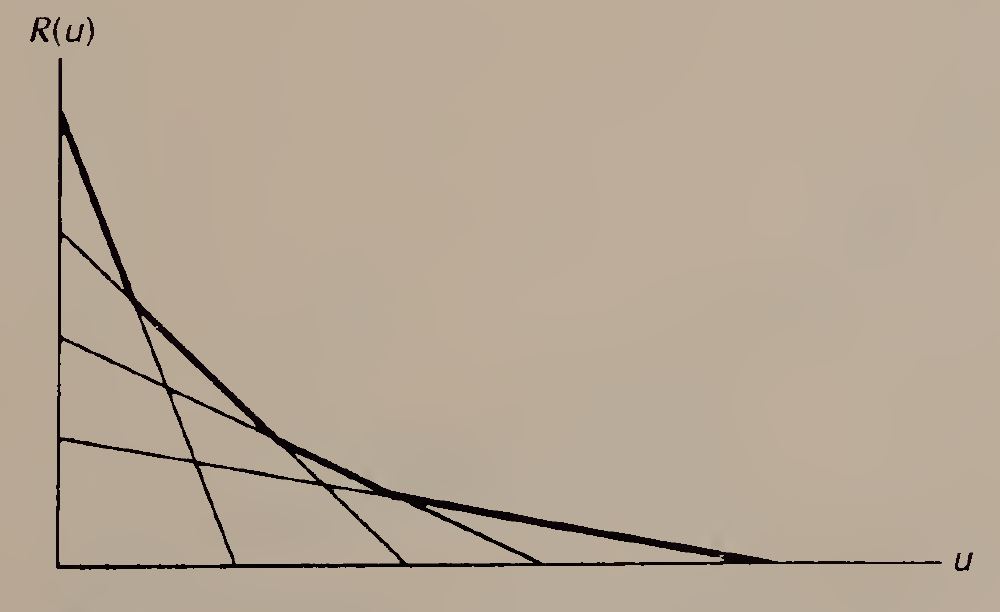 Gráfica 1. Curva envolvente de renta, (Mills y Hamilton, 1984)
Gráfica 1. Curva envolvente de renta, (Mills y Hamilton, 1984)
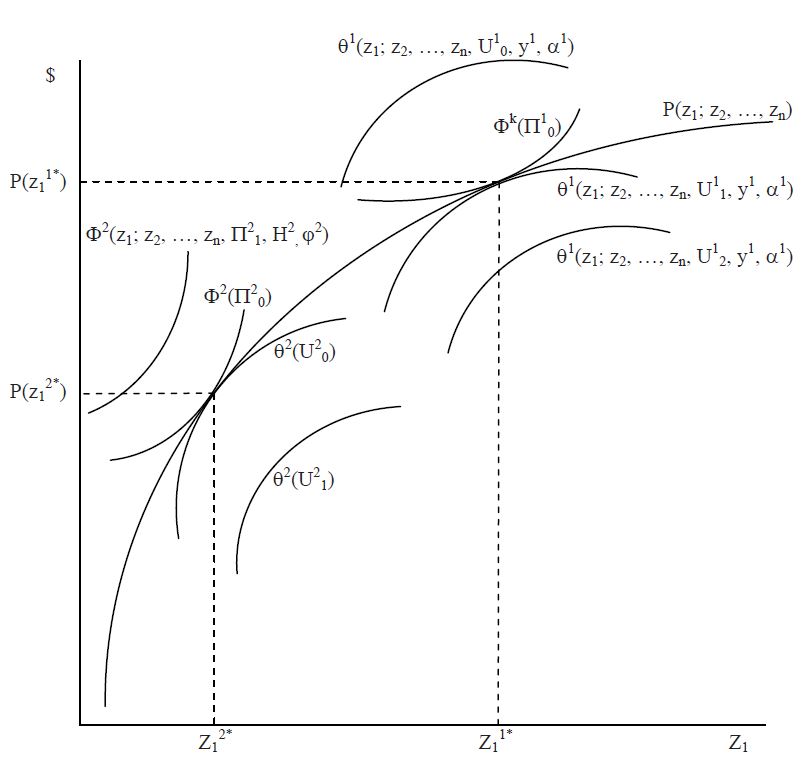 Gráfica 2. Función de Precios Hedónicos, (Taylor, 2008)
Gráfica 2. Función de Precios Hedónicos, (Taylor, 2008)

Consideraciones sobre la información espacial
Consideraciones sobre la información espacial
La estimación de la función de precios se realiza de una variedad de formas. Entre los métodos más usados destaca el uso de regresión lineal múltiple mediante Mínimos Cuadrados Ordinarios (MCO) o máxima verosimilitud (MV) (Taylor, 2008). Comúnmente se emplea una especificación semilogarítmica:
\[ \ln(P_i) = \alpha + \sum_{j=1}^{J} \beta_j Z_{ji} + \varepsilon_i \]
Donde el logaritmo natural del precio de la i-esima vivienda es una función de la j-esima característica que se asume, influye en el precio, Zji son sus atributos, e es el término de error, α y β son los coeficientes estimados.
Sin embargo, los modelos deben cumplir con ciertos supuestos relacionados con el proceso de generación de la información. El más importante se refiere a errores esféricos, es decir, homoscedasticidad, ausencia de autocorrelación, así como una distribución normal de los residuos (𝜖∼𝑁(0,𝜎2)). El incumplimiento de tales restricciones puede provocar que las estimaciones de los parámetros, es decir, los precios marginales implícitos de los atributos dejen de ser confiables (Kauko y D’ Amato, 2008; Turizo, 2024).
Información espacial
La información sobre viviendas, y en general la información georreferenciada o con dimensión espacial se caracteriza por presentar efectos espaciales, los cuales son decisivos y deben ser considerados en análisis econométricos para evitar invalidar los resultados obtenidos. Estos efectos son dos: dependencia espacial, también llamada autocorrelación espacial, y, heterogeneidad espacial o no estacionariedad (Anselin, 1988).
La dependencia espacial se refiere a una relación de dependencia entre observaciones espacialmente cercanas y obedece a la primera ley de Tobler la cual establece que “todo está relacionado con todo, pero las cosas cercanas están más relacionadas” (Tobler, 1970, p.236). En el caso de la vivienda, la dependencia espacial se puede producir por diferentes razones, por un lado, los atributos subjetivos y la idiosincrasia de la colonia o barrio pueden inducir la aglomeración de población con características similares, lo que implica la agrupación de viviendas similares (Wittowsky et al., 2020).
Por otro lado, dado que los barrios suelen desarrollarse al mismo tiempo, las viviendas pueden tener características estructurales muy similares, como el tamaño o el diseño. Además, las viviendas pertenecientes a una misma zona comparten externalidades, tanto positivas como negativas, relacionadas con su ubicación (Basu y Thibodeau 1998; Turizo, 2024). Por lo tanto, las viviendas ubicadas cerca una de la otra frecuentemente están autocorrelacionadas, es decir, sus precios también dependen de los precios de sus vecinos (Cohen y Coughlin, 2008; Wittowsky et al., 2020).
Respecto a la heterogeneidad espacial, esta se refiere a la falta de estabilidad en el comportamiento del fenómeno estudiado a lo largo del espacio. Implica que las formas funcionales y los parámetros cambian con la localización y no son homogéneos en todo el conjunto de datos. Esta condición puede ser provocada por los mismos mecanismos que generan la autocorrelación espacial, aunque no son fenómenos iguales (Anselin, 1988).
Además, la existencia de los efectos espaciales puede provocar relaciones no lineales entre los atributos y el precio. Por ejemplo, las externalidades negativas causadas por la presencia de actividad comercial en estaciones de transporte público, como ruido, contaminación o crimen, pueden provocar que el valor sea menor cerca de la estación, pero después de cierto umbral de distancia el sentido de la relación se invierta debido a la accesibilidad que sigue representado su cercanía (Soltani et al., 2024).
Por estas razones es necesario incorporar los efectos espaciales y relaciones no lineales en los modelos para poder realizar cualquier análisis inferencial fiable (Greenstone, 2017; Kauko y D ’Amato, 2008; Redfearn, 2009). En los últimos años, muchas investigaciones se han enfocado en desarrollar técnicas que permitan superar las limitaciones del método de MCO para el estudio de precios de la vivienda en presencia de efectos espaciales, mejorando su capacidad predictiva y explicativa (Turizo, 2024).
Los campos de la econometría espacial y la geoestadística han proporcionado algunas de las herramientas más utilizadas para modelar efectos espaciales. Entre las más destacadas se encuentran los modelos de autorregresión espacial (SAR) y los modelos de error espacial (SEM), en el caso de la dependencia espacial; y modelos de regresión local y geográficamente ponderada (LWR, GWR), en el caso de la heterogeneidad espacial (Anselin, 1988; Potrawa y Tetereva, 2022; Taylor, 2008).
En estos modelos, para poder manejar la autocorrelación espacial se necesita especificar la forma y el grado de vecindad entre los datos. Para ello, se utiliza una matriz de pesos espaciales, W, que ayuda a establecer relaciones multidireccionales, es decir, la interdependencia entre regiones u observaciones (Anselin, 1988; Turizo, 2024; Taylor, 2008).
La matriz de pesos espaciales es similar al operador de rezago en las series de tiempo, solo que en este caso es multidimensional. Esta define el sentido en el cual las viviendas se consideran vecinas y determina la importancia de las observaciones adyacentes en la conformación del precio. En los estudios de vivienda, las matrices de vecindad y distancia son las especificaciones más comunes de matriz de pesos (Taylor, 2008).
Cabe mencionar que en el modelo de rezago espacial (SAR), los coeficientes estimados β no pueden interpretarse directamente como efectos marginales, debido a la retroalimentación entre unidades vecinas inducida por el término espacial. El efecto de un cambio en una variable independiente sobre la variable dependiente no solo afecta a la observación en cuestión, sino que también se propaga hacia las observaciones vecinas y retorna parcialmente a la unidad original a través de la red espacial definida por la matriz de pesos espaciales (Anselin, 2002; LeSage y Pace, 2009).
Por tanto, los coeficientes 𝛽 representan únicamente los parámetros estructurales del modelo, pero no los impactos marginales reales. Para dar cuenta del efecto real es necesario calcular los efectos directos, indirectos y totales. Los efectos directos se obtienen como el promedio de los impactos que un cambio en la variable independiente xi tiene sobre la variable dependiente yi en la misma unidad, incluyendo los efectos de retroalimentación. Es decir, el efecto directo refleja no solo el efecto propio, sino también el efecto que el incremento en la variable dependiente de una unidad genera en sus vecinas y que, a su vez, retorna a la unidad original (LeSage y Pace, 2009).
Por su parte, los efectos indirectos reflejan el impacto que se transmite espacialmente entre observaciones debido a la estructura de dependencia definida por la matriz de pesos espaciales. Captura los efectos de externalidades, es decir, como un cambio en xi afecta a yj, (con j≠i) a través de las interconexiones espaciales (LeSage y Pace, 2009).
Los efectos totales son la suma de los efectos directo e indirecto y reflejan el impacto completo en todo el sistema ante un cambio en la variable independiente, teniendo en cuenta las dependencias espaciales. En el modelo SAR, estos impactos se calculan a partir de la siguiente expresión:
\[ \frac{\partial y}{\partial X_r} = (I - \rho W)^{-1} \beta_r \]
Esta matriz indica que el efecto total de un cambio marginal en xr sobre y es igual al producto del coeficiente 𝛽r por el multiplicador espacial (𝐼−𝜌𝑊)−1. A partir de esta matriz se pueden obtener el efecto directo y el efecto indirecto. Esta descomposición ofrece una interpretación más adecuada del impacto espacial en fenómenos como la formación de precios de la vivienda, donde las condiciones del entorno tienen un papel relevante (LeSage y Pace, 2009).
Este abanico de herramientas ha sido ampliamente usado para estimar la FPH, es decir, la estimación de los precios marginales implícitos de los atributos que componen la vivienda. Sus resultados muestran la importancia de incluir en los modelos los efectos espaciales y las relaciones complejas y no linealidades, con el objetivo de obtener estimadores confiables e información más detallada sobre los fenómenos subyacentes.
A pesar de los avances tecnicos, estos metodos aun contienen ciertas limitaciones, la principal de ellas es la imposibilidad de dar cuenta de relaciones no lineales o complejas. Recientemente, algunos investigadores han considerado utilizar la habilidad natural de los modelos de aprendizaje automático de capturar no linealidades y entender con mayor detalle las relaciones existentes. En la última década, se han desarrollado avances técnicos que habilitan la interpretación de las relaciones aprendidas por los algoritmos, brindando la posibilidad de una descripción más detallada de las relaciones que existen entre las características de la vivienda y su precio.
.jpg)
.jpg) Información espacial
Información espacial

IA para el análisis inmobiliario
IA para el análisis inmobiliario
Gracias a la creciente adopción de sistemas de inteligencia artificial en la toma de desiciones públicas, en años recientes han surgido leyes y reglamentos que exigen que los algoritmos de aprendizaje automático sean justos, transparentes y explicables. Algunos ejemplos son la Regulación General de Protección de Datos de la Unión Europea, publicada en 2016 o el programa de Inteligencia Artificial Explicable (XIA), de la Agencia de Proyectos de Investigación Avanzada de Defensa de Estados Unidos (DARPA), publicado en 2017, que fueron elaborados con el objetivo de avanzar en las técnicas de aprendizaje automático para producir modelos interpretables sin sacrificar el rendimiento y permitir que los usuarios comprendan, confíen y gestionen adecuadamente la generación de sistemas de inteligencia artificial (Li, 2022).
La emergencia de metodos para volver interpretables los modelos abre la posibilidad de conseguir indicios más completos y matizados sobre las relaciones complejas (no lineales) existentes en el mercado de vivienda, las cuales no pueden ser capturados por enfoques paramétricos tradicionales. Con su avance, los algoritmos de aprendizaje automático dejan de ser cajas negras y se vuelve posible aprovechar su flexibilidad y habilidad predictiva para realizar análisis detallados sobre las relaciones entre variables, por ejemplo, en la estimación de la primera fase hedónica y beneficiarse de su capacidad de aprender relaciones entre los atributos y el precio (Rico-Juan & Taltavull De La Paz, 2021).
Existen dos formas de interpretar los resultado de los modelos de aprendizaje automatico. Por un lado mediante la reducción en complejidad de los modelos, lo que implica tambien la perdida de su superioridad predictiva; por otro lado, mediante el uso de marcos explicativos separados de los modelos de aprendizaje automático, también denominados modelos agnósticos de interpretabilidad. Estos métodos permiten preservar la capacidad predictiva de los modelos, y al mismo tiempo extraer información interpretable de las relaciones aprendidas. Son muy flexibles ya que no dependen de un algoritmo de aprendizaje automático específico, sino que pueden ser aplicados a cualquiera, independientemente de su mecanismo de funcionamiento (Du et al., 2025; Molnar, 2020; Rico-Juan y Taltavull De La Paz, 2021).
Con estos metodos se puede extraer tres tipos de datos. En primer lugar, la importancia de las variables (FI) la cual, mediante la comparación del cambio en la magnitud del efecto en la predicción, ante cambios en los valores de las variables de interés, permite identificar las características más importantes en la conformación del valor predicho. En segundo lugar, la dependencia parcial (PD), la cual es una herramienta gráfica que muestra los efectos marginales de una característica particular sobre el valor predicho por el modelo en todo su rango. Un metodo para calcular esta dependencia parcial es mediante los Efectos Locales Acumulados (ALE), los cuales tienen la ventaja, ante otros métodos, de ser robustos ante la presencia de multicolinealidad, común en la información espacial (Y. Wu y Han, 2025).
En tercer lugar, existen los modelos de interpretación local, como las explicaciones Shapley aditivas, (SHAP) o las explicaciones locales interpretables, (LIME), los cuales muestran el efecto de cada variable en una observación particular (Jin et al., 2023; Lundberg y Lee, 2017; Molnar 2020; Ribeiro et al., 2016). En el caso de los valores SHAP, para su estimación se utilizan conceptos analíticos de la teoría de juegos que permiten identificar la contribución individual de cada variable en el resultado final, por lo que es considerado un método confiable y robusto para extraer efectos individuales. Por su parte, los valores LIME utilizan modelos locales lineales para estimar los efectos de las variables. Este último tipo tiene ciertas similitudes con los modelos GWR en el sentido de tener que definir una ventana de observaciones, aunque en este caso, son observaciones cercanas en un plano vectorial (Lundberg y Lee, 2017; Molnar, 2020).
Aplicación en la metodología hedónica
En el marco de la metodología hedónica, estos metodos representan nuevas formas de estimar la Función de Precios Hedónicos e incluso la posibilidad conocer los efectos de los atributos en viviendas individuales. En la última década, algunos investigadores han experimentado con su aplicación en la estimación de la primera fase hedónica, mostrando resultados prometedores respecto a la identificación de relaciones complejas.
Sin embargo, a pesar de sus ventajas, también están limitados en ciertos aspectos. En primer lugar, son métodos no paramétricos, meramente exploratorios y descriptivos. Aunque pueden evaluar qué variables contribuyen más a la predicción y ofrecen métricas de desempeño como el R2 o la raíz del error cuadrático medio (RMSE) para estimar la bondad de ajuste del modelo, no están diseñados para realizar inferencia estadística en el sentido tradicional. Es decir, no proporcionan estimaciones puntuales de coeficientes acompañadas de errores estándar, intervalos de confianza o valores p que permitan evaluar la significancia estadística a de los predictores. Estos componentes están relacionados con la inferencia estadística y permiten valorar, por ejemplo, que la probabilidad real en la población sea distinta de cero. Por este motivo, estos modelos no permiten realizar inferencias causales directas y su aplicación debe considerarse principalmente exploratoria (Iskhakov et al., 2020).
En segundo lugar, algunos modelos se ven afectados por la correlación entre variables, como por ejemplo el modelo LIME o la dependencia parcial, aunque métodos de cálculo como ALE superan estos límites (Li, 2022; Molnar, 2020; Potrawa y Tetereva, 2022).
Finalmente, a pesar de la flexibilidad y capacidad de aprender relaciones en los datos, los modelos de aprendizaje automático no consideran ningún efecto espacial(Kopczewska, 2022). No atender a los efectos espaciales genera problemas como ajustes demasiado optimistas de los modelos, información omitida o predicciones subóptimas, aspectos discutidos en párrafos anteriores (Heng et al., 2018). Sin embargo, para capturar las relaciones espaciales basta con introducir en el modelo variables que den cuenta de ellas. Algunos ejemplos pueden ser coordenadas geográficas, distancias a puntos específicos de la ciudad, e incluso una variable espacialmente rezagada idéntica a la utilizada en los modelos de econometría espacial. Atender el problema de autocorrelación permite no solo reproducir los datos de entrenamientos, sino también realizar predicciones en nuevas ubicaciones fuera del conjunto de datos (Jin et al 2023).
 IA en el análisis inmobiliario
IA en el análisis inmobiliario
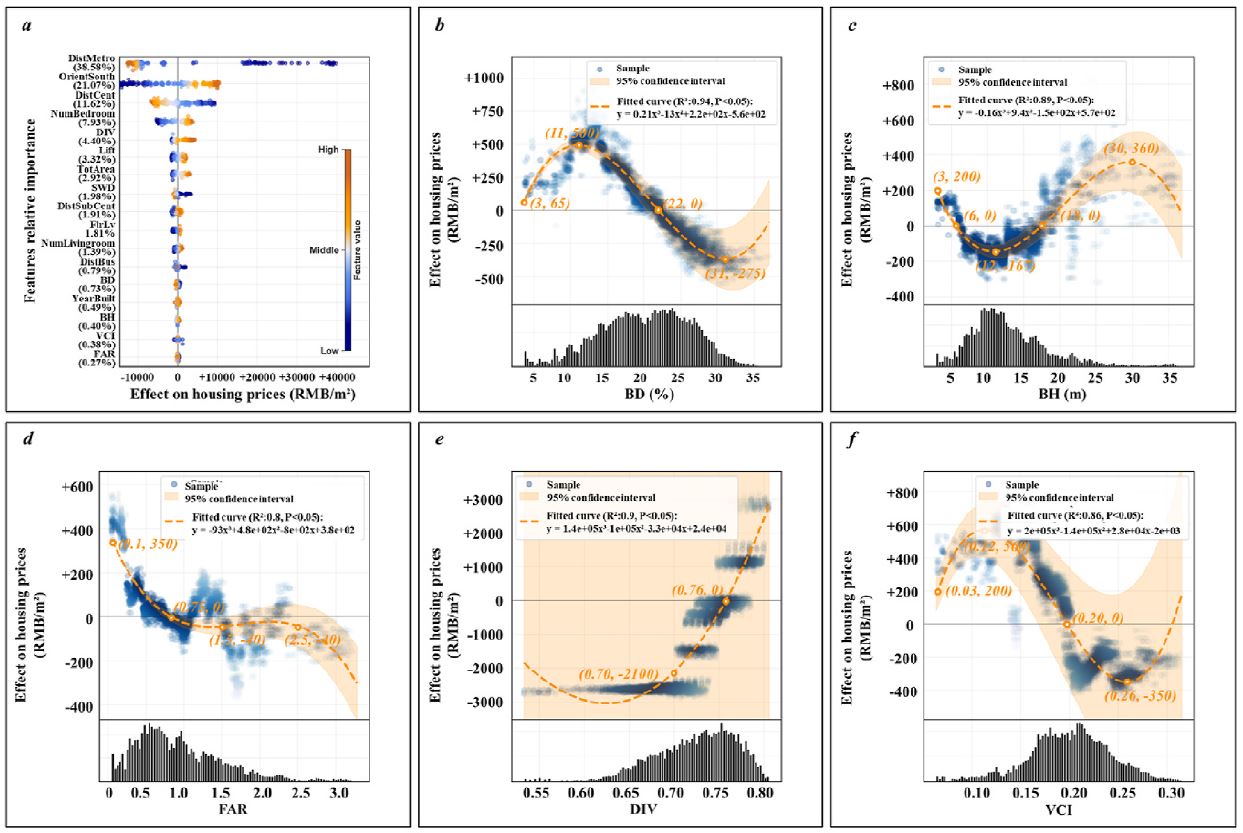 Feature importance & Partial dependence, Liu et al., 2024.
Feature importance & Partial dependence, Liu et al., 2024.
 Acumulated Local Effects (ALE), Potrawa & Tetereva, 2022.
Acumulated Local Effects (ALE), Potrawa & Tetereva, 2022.
 SHAP, Ziqi Li, 2022
SHAP, Ziqi Li, 2022

Metodología
Metodología
Los datos sobre el mercado inmobiliario se obtuvieron mediante el uso de la técnica de rascado de datos tambien conocida como "webscrapping" usando páginas web sobre clasificados inmobiliarios. La información obtenida consiste únicamente en publicaciones de casas en venta, disponibles en internet del 16 al 20 de abril de 2025. La información corresponde a la Ciudad de México y los municipios que conforman a la ZMCM, siendo un total de 10,802 observaciones.
La información contiene datos sobre la estructura de las viviendas y su localización en coordenadas, lo que permite capturar una gran diversidad de características físicas y contextuales.
Las variables usadas para potencialmente caracterizar el vecindario se construyeron utilizando información del Censo de Población y Vivienda, 2020 (CPyV) del INEGI. Con herramientas de análisis espacial, se extrajo información sociodemográfica sobreponiendo la capa de puntos de viviendas a la información vectorial a nivel manzana del censo, de tal forma que se agregó la información del censo, de la manzana en donde se localiza la vivienda, a la base de datos de puntos como una nueva columna (Mapa 2). Los campos extraídos del censo fueron: población total y grado promedio de escolaridad. Esta información fue utilizada para construir dos variables, las cuales son densidad de población y grado promedio de escolaridad, que se incluyeron en la categoría localización.
Respecto a la caracterización del entorno urbano, puede realizarse mediante diferentes métodos. En este trabajo se seleccionó el método multibanda ya que permite mantener la capacidad de estimar relaciones complejas, manteniendo simple la interpretación y reduciendo el costo computacional de su implementación. Además, es un método ampliamente usado y recomendado en los análisis de precios hedónicos que estiman la relación con los elementos externos a la vivienda (Basu y Thibodeau, 1998).
Los elementos urbanos considerados son, por un lado, infraestructura de movilidad como estaciones y rutas del sistema de transporte público de la ZMCM. La información es de tipo vectorial y fue obtenida de la página de datos abiertos del gobierno de la Ciudad de México y la página de la Secretaría de Transporte y Movilidad del Estado de México. Las infraestructuras abarcan estaciones de Metro, Tren Ligero, Tren Suburbano, Teleférico (Cablebus y Mexicable), RTP, BRT (Metrobús y Mexibús), CETRAM, Ecobici, Biciestacionamientos y Trolebús; Rutas de Transporte Concesionado, Líneas de Ciclovía; y Aeropuertos.
Por otro lado, tambien se consideraron equipamientos urbanos cuya información de igual forma es de tipo vectorial y se obtuvo del Directorio Estadístico Nacional de Unidades Económicas (DENUE) del INEGI. Las actividades tomadas en cuenta para el análisis son aquellos equipamientos de carácter público que proveen servicios como: Educación, Salud, Recreación, Cultura y Deporte y Oficinas de Gobierno.
Las bandas se construyeron mediante buffers alrededor de los elementos urbanos, de tal forma que cada variable de accesibilidad a un elemento urbano específico contiene 20 anillos o rangos de distancia, cuyos valores son: 0-50, 100, 200, 300, 450, 600, 800, 1,100, 1,500, 2,000, 3,000, 5,000, 8,000, 12,000, 17,000, 23,000, 30,000, 38,000, 47,000 y 60,000 metros. La elección de estas distancias se basa en la expectativa teórica de que a distancias cortas los efectos de los elementos son más intensos y variados, siguiendo la primera ley de Todler, por lo que los anillos capturan más variaciones a distancias cortas.
Al igual que con la información vectorial del censo de población, la capa de puntos se sobrepuso a la capa de bandas y se extrajo el valor de la banda en que se localiza cada vivienda. Cabe decir que, en la creación de las bandas, los bordes se diluyeron, por lo que no existe sobreposición de bandas y la variable resultante representa la distancia al elemento urbano de interés más cercano. El valor que se extrae es la distancia media entre el límite superior e inferior de la banda.
Finalmente, para las variables de localización se incluyó la distancia al DCN y al centro financiero de Santa Fe. Estos fueron tomados del trabajo de Muñiz et al, 2015, quienes realizaron un ejercicio de identificación de centros y subcentros de empleo mediante métodos estadísticos rigurosos. Sin embargo, en el presente trabajo solo se consideraron el DCN y el subcentro de Santa Fe para simplificar el análisis. También se incluyó una variable espacialmente rezagada con la variable dependiente, tanto en los modelos de econometría espacial, como los modelos de aprendizaje automático, la cual fue calculada con una matriz de pesos espaciales construida con el método k vecinos más cercanos = 10.
La variable de respuesta utilizada en el análisis es la transformación logarítmica del precio de la vivienda, debido a que la distribución de la variable “precio” está fuertemente sesgada a la derecha y a que la variable logarítmica mostró un mejor ajuste en todos los modelos. Por su parte, las variables independientes fueron estandarizadas en los modelos paramétricos MCO y SAR para facilitar su comparabilidad. Sin embargo, en los modelos de aprendizaje automático, debido a la flexibilidad que los caracteriza y con el objetivo de simplificar la interpretación de los resultados en el contexto de relaciones no lineales, se utilizaron los valores absolutos de las variables independientes
El análisis empírico de los determinantes del precio consistió en la aplicación modelos de regresión para estimar la primera fase de la metodología hedónica o estimación de la Función de Precios Hedónicos. Para una estimación consistente se utilizaron diversas herramientas estadísticas. Primero, se estimaron pruebas de multicolinealidad y se seleccionaron las variables con menor correlación. Posteriormente, se estimó un modelo base de MCO bajo los principios de parsimonia con las variables seleccionadas, cuyos errores se analizaron mediante diversas pruebas estadísticas para buscar indicios autocorrelación espacial y verificar el cumplimiento de los supuestos clave para estimar coeficientes confiables.
Con los resultados obtenidos en esta etapa se justificó el uso de modelos espaciales y se estimaron modelos SAR y SEM los cuales se compararon mediante las medidas de bondad de ajuste R2, AIC, BIC, y Log-likelihood para determinar el mejor modelo. Los coeficientes del modelo seleccionado (SAR) se interpretaron considerando las implicaciones de la dependencia espacial. Por tal motivo, se calcularon los efectos directos, indirectos y totales, que reflejan el impacto completo de las variables explicativas, teniendo en cuenta las interdependencias espaciales, y se interpretaron conforme a lo expuesto en la sección teórica (LeSage y Pace, 2009).
Adicionalmente, con un espíritu exploratorio, se estimaron modelos de aprendizaje automático y se aplicaron modelos agnósticos de interpretabilidad para mostrar la dependencia parcial y las contribuciones locales de las variables. La dependencia parcial de las variables se calculó mediante ALE, que permite identificar efectos marginales promedio a lo largo del rango de cada variable, ofreciendo un puente entre los coeficientes globales de los modelos econométricos y las relaciones complejas capturadas por los modelos de aprendizaje automático. Por su parte, las contribuciones locales se calcularon con el uso de valores SHAP, los cuales permiten observar las contribuciones individuales de cada variable en las predicciones del modelo, descomponiendo su valor estimado para cada vivienda.
Este enfoque permite identificar patrones no lineales y variaciones locales sin necesidad de fragmentar el espacio urbano ni imponer supuestos paramétricos. De esta manera, mientras los modelos espaciales permiten captar estructuras y dependencias globales, las técnicas de aprendizaje automático aportan una perspectiva más flexible, detallada y localizada, revelando matices y complejidades que suelen quedar fuera del alcance de los métodos paramétricos tradicionales.
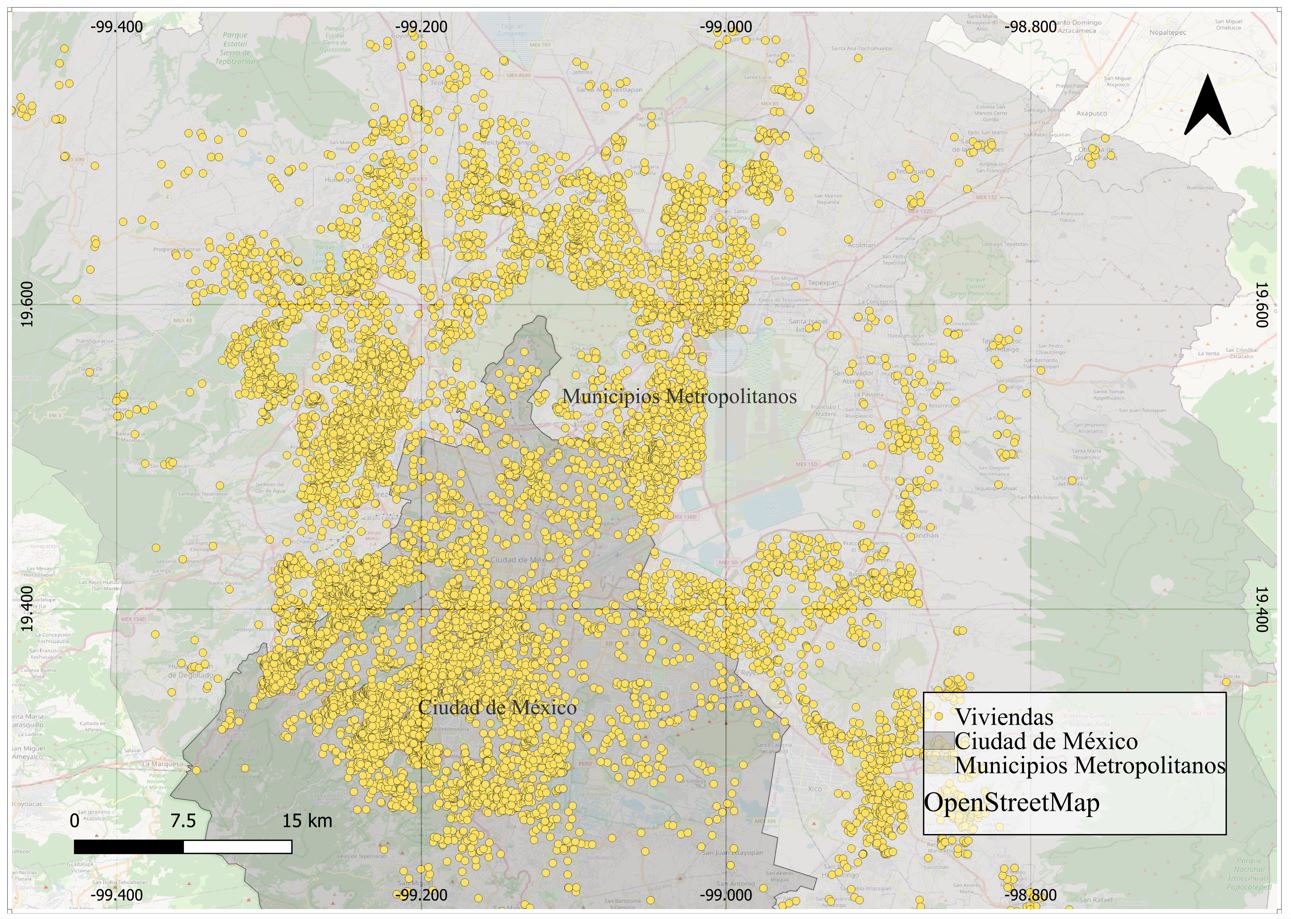 Mapa 1. Distribución espacial de la muestra
Mapa 1. Distribución espacial de la muestra
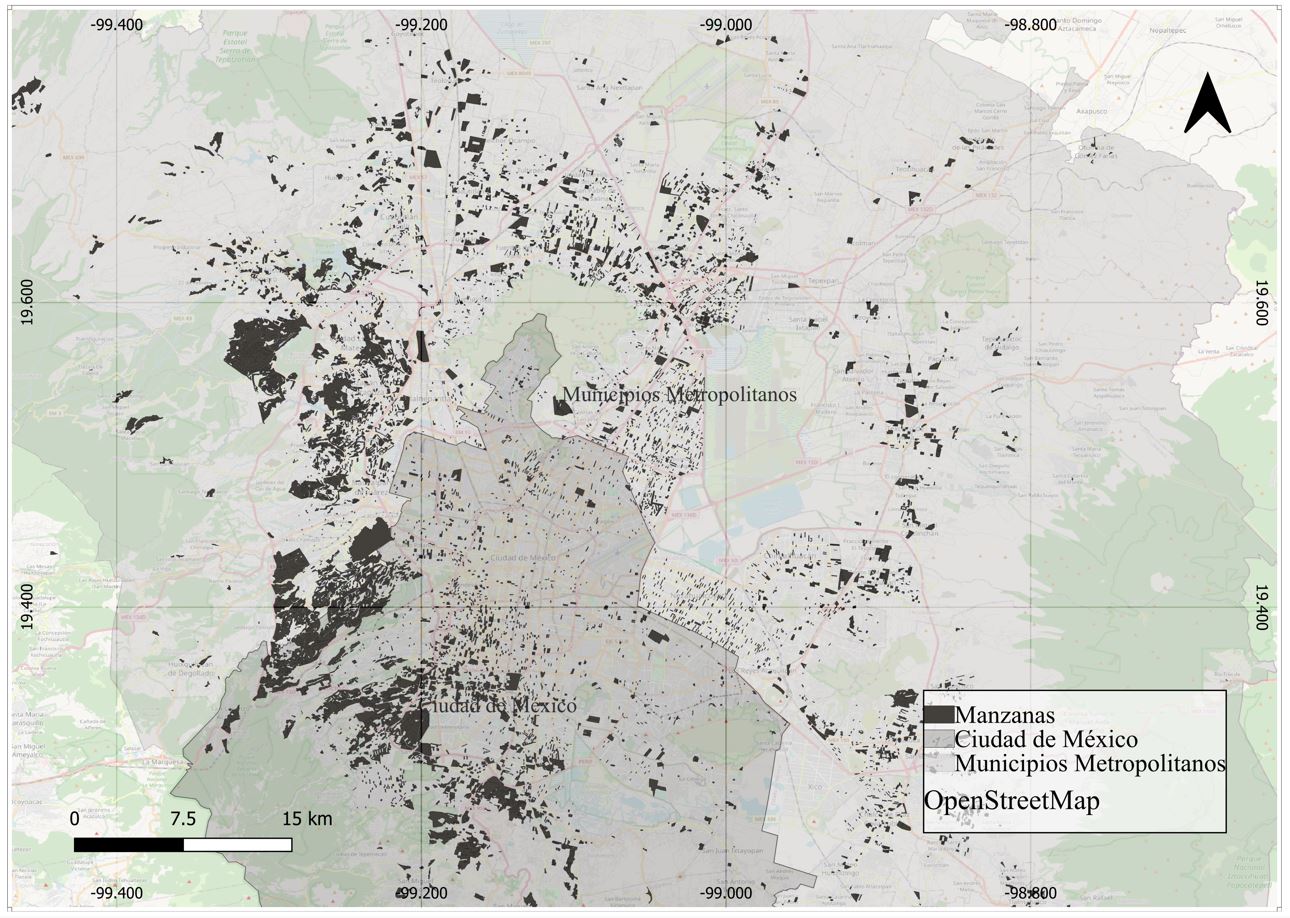 Mapa 2. Manzanas de la muestra
Mapa 2. Manzanas de la muestra
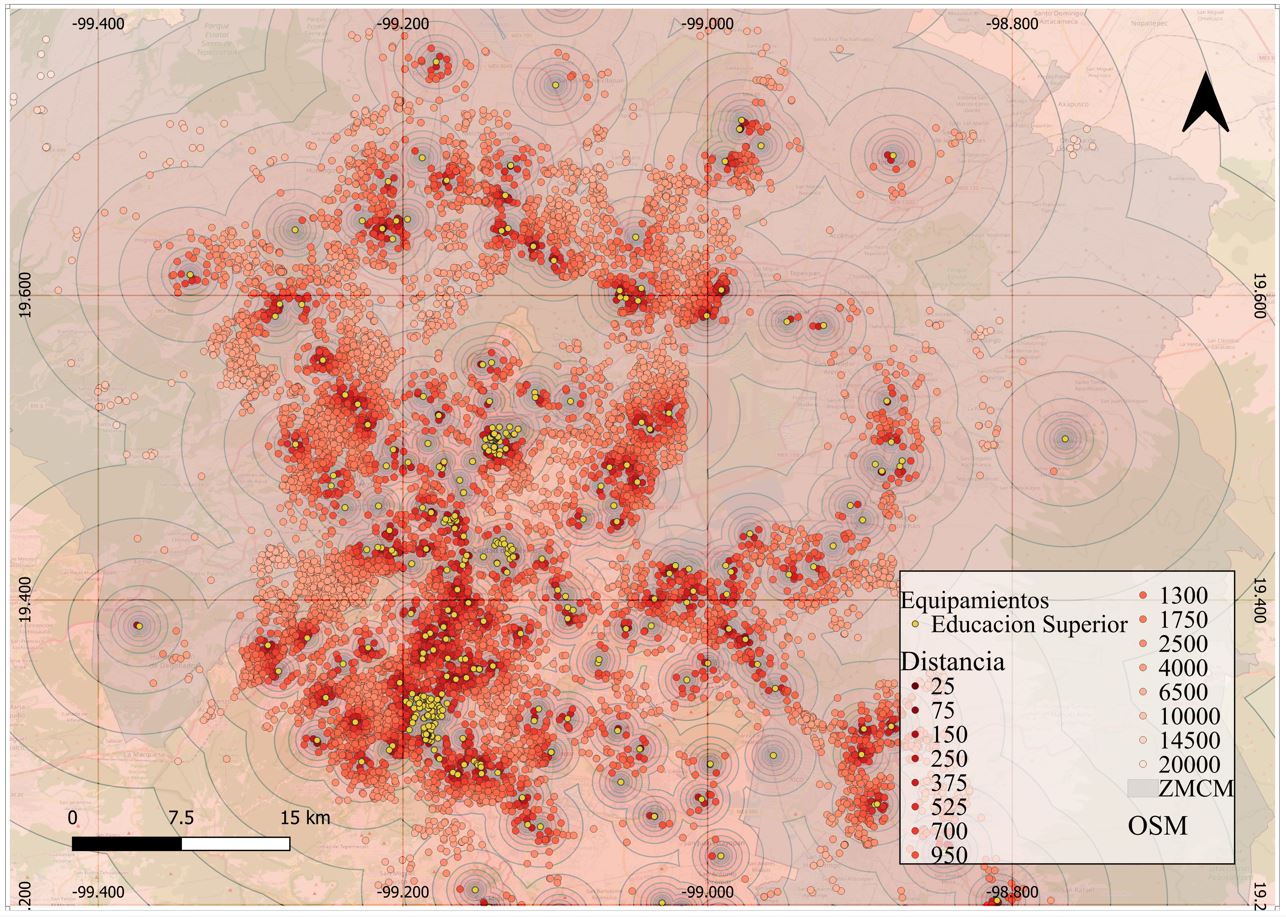 Mapa 3. Bandas de distancia, Educación Superior
Mapa 3. Bandas de distancia, Educación Superior
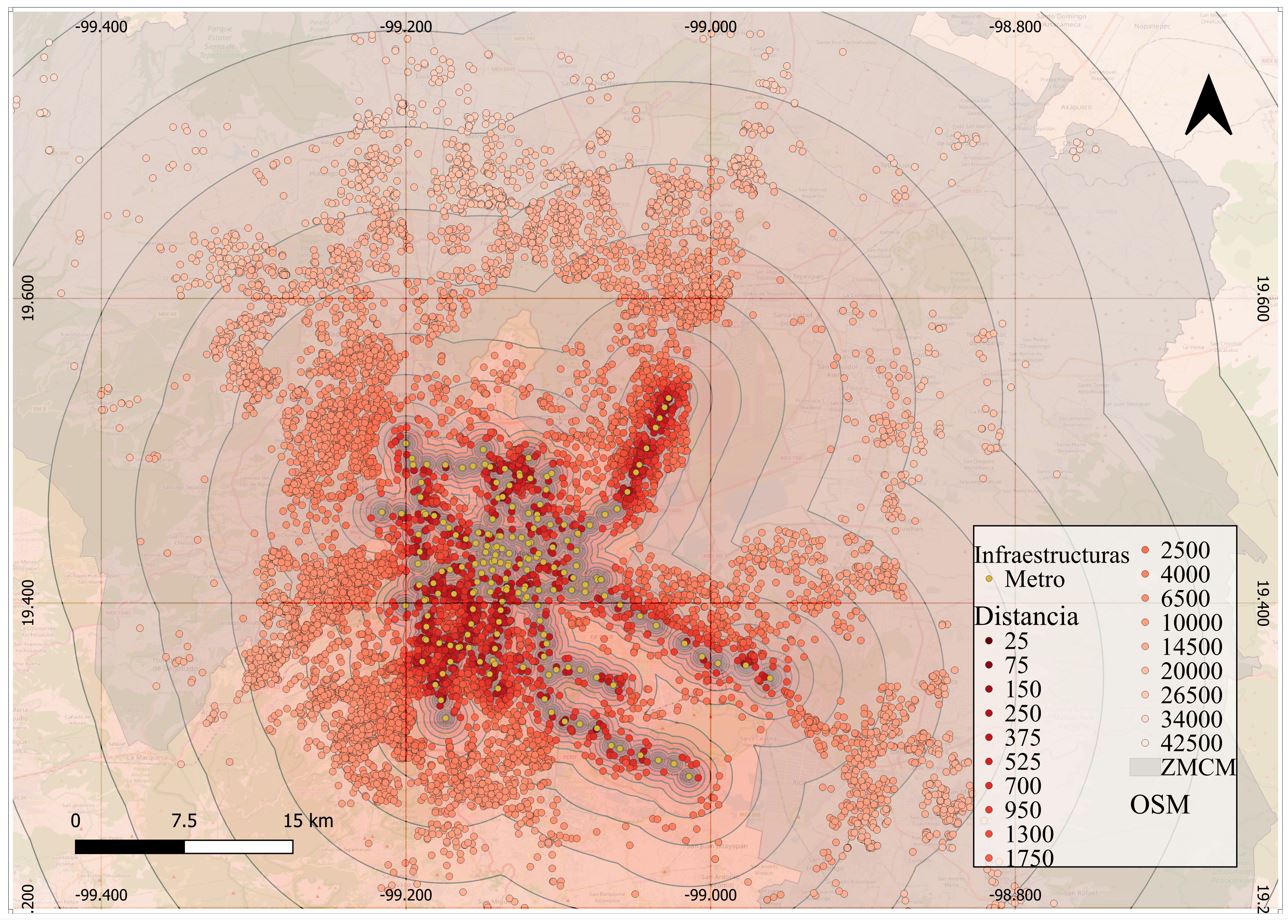 Mapa 4. Bandas de distancia, Metro
Mapa 4. Bandas de distancia, Metro
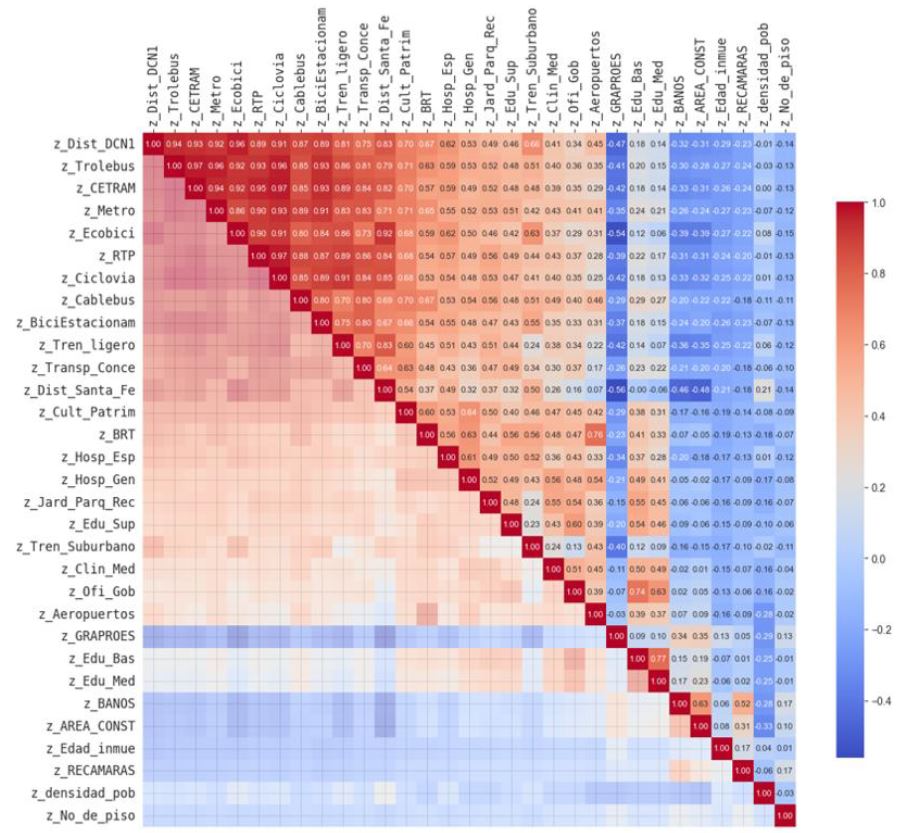 Matriz de correlación
Matriz de correlación
Hallazgos principales
Resultados del modelo de regresión
| Variable | Coeficiente | Error estándar | Estadístico Z | Efecto directo | Efecto indirecto | Efecto total |
|---|---|---|---|---|---|---|
| CONSTANT | 7.97152*** | 0.12836 | 62.10476 | - | - | - |
| z_RECAMARAS | 0.0443*** | 0.00566 | 7.82589 | 0.0443 | 0.0414 | 0.0857 |
| z_No_de_piso | 0.01633*** | 0.00439 | 3.71899 | 0.0163 | 0.0153 | 0.0316 |
| z_BANOS | 0.11591*** | 0.00648 | 17.8906 | 0.1159 | 0.1083 | 0.2242 |
| z_AREA_CONST | 0.40655*** | 0.00646 | 62.90103 | 0.4066 | 0.3798 | 0.7864 |
| z_Edad_inmue | 0.02437*** | 0.00426 | 5.71683 | 0.0244 | 0.0228 | 0.0471 |
| Jardin | 0.01442 | 0.00891 | 1.6186 | 0.0144 | 0.0135 | 0.0279 |
| terraza | 0.08745*** | 0.01076 | 8.12713 | 0.0875 | 0.0817 | 0.1692 |
| z_GRAPROES | 0.06977*** | 0.00561 | 12.43936 | 0.0698 | 0.0652 | 0.1349 |
| z_densidad_pob | -0.06298*** | 0.00516 | -12.20433 | -0.063 | -0.0588 | -0.1218 |
| z_Aeropuertos | 0.02612*** | 0.00767 | 3.4051 | 0.0261 | 0.0244 | 0.0505 |
| z_BiciEstacionam | 0.05157*** | 0.01006 | 5.12352 | 0.0516 | 0.0482 | 0.0997 |
| z_BRT | 0.02809*** | 0.00879 | 3.19341 | 0.0281 | 0.0262 | 0.0543 |
| z_Teleférico | -0.02891*** | 0.00998 | -2.89671 | -0.0289 | -0.027 | -0.0559 |
| z_Tren_ligero | -0.16968*** | 0.01018 | -16.66774 | -0.1697 | -0.1585 | -0.3282 |
| z_Tren_Suburbano | -0.09084*** | 0.00738 | -12.31333 | -0.0908 | -0.0849 | -0.1757 |
| z_Transp_Conce | 0.05003*** | 0.00962 | 5.20253 | 0.05 | 0.0467 | 0.0968 |
| z_Clin_Med | -0.00108 | 0.00585 | -0.18388 | -0.0011 | -0.001 | -0.0021 |
| z_Hosp_Gen | 0.01864*** | 0.00686 | 2.71703 | 0.0186 | 0.0174 | 0.0361 |
| z_Hosp_Esp | 0.01131* | 0.00648 | 1.74469 | 0.0113 | 0.0106 | 0.0219 |
| z_Edu_Bas | 0.01851** | 0.00837 | 2.21155 | 0.0185 | 0.0173 | 0.0358 |
| z_Edu_Med | -0.00329 | 0.00699 | -0.4708 | -0.0033 | -0.0031 | -0.0064 |
| z_Edu_Sup | -0.03785*** | 0.00633 | -5.97764 | -0.0379 | -0.0354 | -0.0732 |
| z_Cult_Patrim | -0.01665** | 0.00703 | -2.36736 | -0.0166 | -0.0156 | -0.0322 |
| z_Jard_Parq_Rec | 0.02641*** | 0.00619 | 4.26405 | 0.0264 | 0.0247 | 0.0511 |
| z_Ofi_Gob | -0.01291* | 0.00699 | -1.84698 | -0.0129 | -0.0121 | -0.025 |
| W_ln_precio | 0.48301*** | 0.00833 | 58.00712 | - | - | - |
*** si p ≤ 0.01 ** si 0.01 < p ≤ 0.05 * si 0.05 < p ≤ 0.10
Los hallazgos sugieren que el valor de la vivienda no depende únicamente de atributos físicos o de la proximidad a elementos urbanos, sino también de su inserción histórica y territorial. Los resultados confirman que existe una fuerte dependencia espacial en los precios de las viviendas (Mapa 6), lo que indica que los valores inmobiliarios no se determinan de manera aislada, sino que se influyen mutuamente, consolidando jerarquías urbanas y sociales.
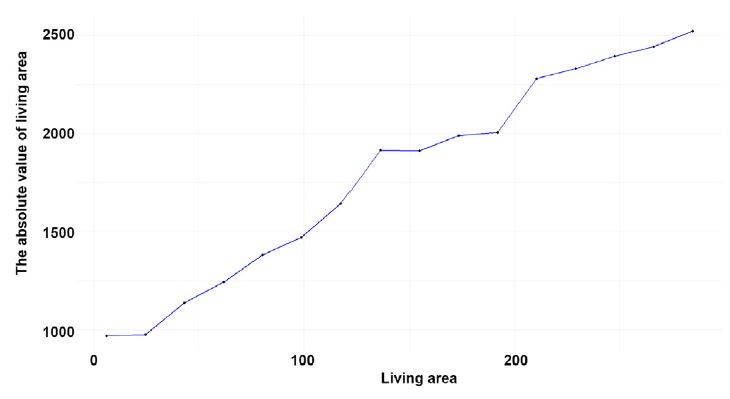
El sur-poniente de la ciudad concentra propiedades de muy alto precio, mientras que las extensas periferias norte y oriente viviendas de menor valor. El tamaño emerge como el factor más influyente en el valor de la vivienda, algo intuitivamente esperable. Sin embargo, las gráficas ALE revelaron que el efecto no es lineal sino decreciente, es decir que cada metro adicional aporta menor valor relativo. Por su parte, las variables de calidad también contribuyen de forma significativa, con incrementos de hasta 16% en el valor dada la presencia de amenidades como terrazas.
La edad del inmueble muestra un efecto complejo. Aunque parece existir una tendencia a la valorización de edificios antiguos, los primeros 15 años parecen reducir el precio de los inmuebles. El efecto positivo puede estar relacionado con valorizaciones históricas del suelo o con su importancia en términos de patrimonio histórico, como sucede en otras ciudades del mundo. Por su parte el efecto negativo puede estar asociado a la concentracion de viviendas de estos rangos de edad en las zonas perifericas, caracterizadas por precios bajos. Las variables del vecindario también muestran efectos importantes. Manzanas con un mayor promedio de años de escolaridad se asocian con incrementos en el valor de 13%, mientras que una mayor densidad de población lo disminuye hasta en 12%.
En cuanto a los elementos urbanos, los resultados reflejan fenómenos diferenciados. Por un lado, la cercania a ciertas infraestructuras y equipamientos muestra un efecto positivo en el precios, explicado por los beneficios que brinda en términos de accesibilidad, como es el caso del Tren Suburbano y Tren ligero con incrementos del 17% y 32% respectivamente; o por ser referentes simbólicos positivos como el caso de las universidades y los equipamientos culturales y patrimoniales con incrementos del 7% y 3% respectivamente. Por otro lado, algunos elementos muestran un efecto negativo en el precio, como las escuelas de educación básica (-3%), hospitales de especialidad (-2%), y aeropuertos (-5%), lo que sugiere que sus efectos están medidos por externalidades negativas como ruido, tráfico, contaminación, restricciones de zonificación o percepción de inseguridad.
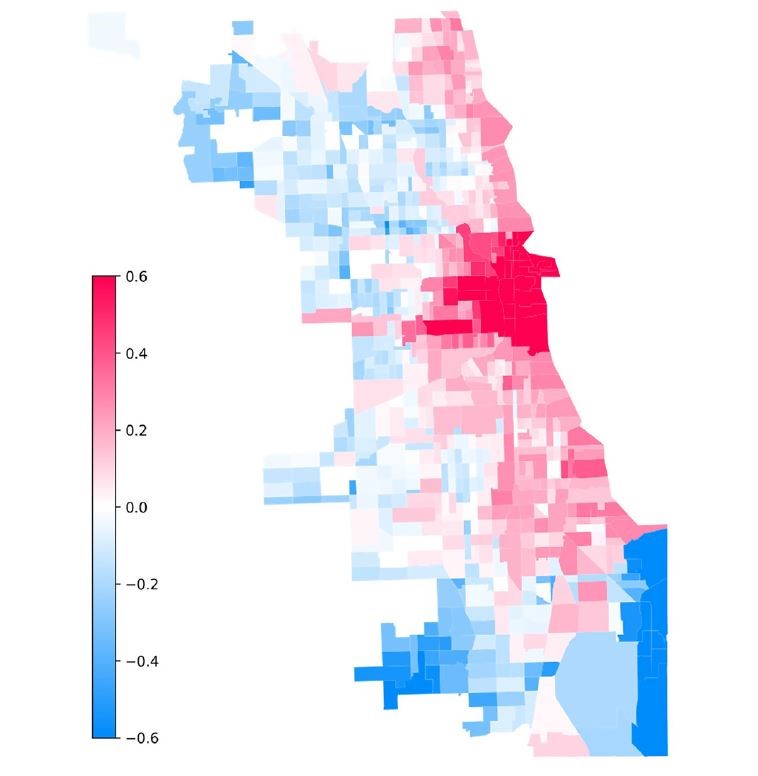
Adicionalmente, ciertas infraestructuras, como el Tren ligero y estaciones de Cablebus, muestran un fuerte componente de dependencia espacial y efectos heterogéneos en el territorio. Los resultados obtenidos con las contribuciones individuales SHAP sugieren una mayor valorización asociada a lugares donde los precios ya son altos. Colonias como Lomas de Chapultepec, Polanco, Jardines del Pedregal, Condesa, Roma, Coyoacán, Del Valle y San Ángel, tradicionalmente asociadas a clases acomodadas, que concentran la mayoría de las viviendas de alto valor y que han sido beneficiadas por una mayor acumulación de inversión pública, se muestran como las más beneficiadas por estas obras de infraestructura. Este fenómeno refuerza la hipótesis de que la magnitud de la capitalización de la inversión pública depende en gran medida de su localización y, particularmente, de su proximidad a zonas donde los precios ya son elevados y, en el caso de la ZMVM, donde históricamente se ha concentrado la inversión pública.
Estos resultados sugieren que el efecto de los elementos urbanos en el valor de una vivienda no depende únicamente de la proximidad física, sino también de cómo dicha infraestructura se articula con otras condiciones urbanas. Los efectos diferenciados en función de la localización pueden interpretarse como expresiones de desigualdad urbana. Algunas obras refuerzan centralidades consolidadas, mientras que otras, aunque funcionales, no consiguen superar estigmas territoriales ni condiciones estructurales que limitan su capacidad para valorizar el entorno.
En conjunto, estos resultados muestran que la valorización del entorno urbano no puede entenderse únicamente desde sus funciones o servicios, sino que está profundamente condicionada por el contexto espacial e histórico en que se inserta, así como por patrones de dependencia espacial que refuerzan desigualdades preexistentes en la ZMCM.
Este trabajo contribuye al entendimiento del mercado de vivienda desde una perspectiva integrada, ya que combina modelos econométricos espaciales con herramientas agnósticas de interpretabilidad.
No obstante, el análisis también enfrenta ciertas limitaciones. La información utilizada refleja un corte estático en el tiempo, lo cual impide capturar dinámicas temporales en la formación de precios o los efectos de intervenciones recientes. También, presenta cierto sesgo hacia segmentos de medio y alto valor, por lo que es necesario integrar información de otras fuentes de datos para ampliar los alcances del análisis.
Además, la identificación de efectos individuales se ve dificultada por la fuerte concentración de infraestructura, lo que motiva la necesidad de complementar estos enfoques con métodos cuasi experimentales o longitudinales. Futuros estudios podrían integrar datos panel, evaluar intervenciones específicas mediante diseños de tipo diferencias en diferencias o profundizar en la valoración de externalidades con modelos causales. Estos enfoques permitirían estimar el impacto específico de nuevas infraestructuras, distinguir efectos temporales y evaluar desigualdades con mayor precisión. Estas líneas de investigación permitirían avanzar hacia una evaluación más precisa del impacto urbano de las infraestructuras y reforzar el vínculo entre investigación y políticas públicas.
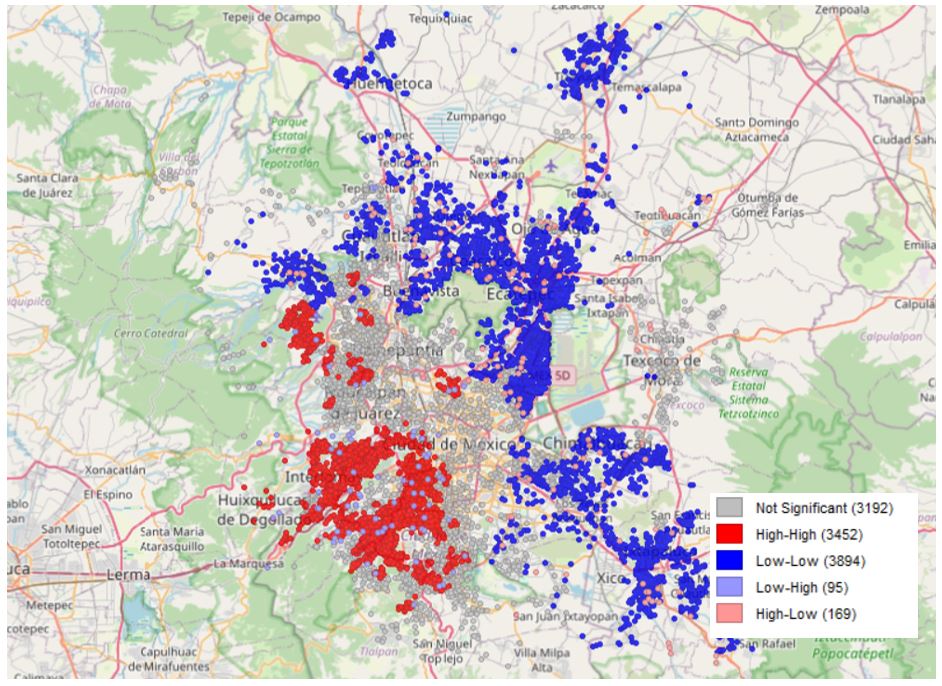 Mapa 6. Índice de Autocorrelación Espacial Local I Moran (Ln_precio)
Mapa 6. Índice de Autocorrelación Espacial Local I Moran (Ln_precio)
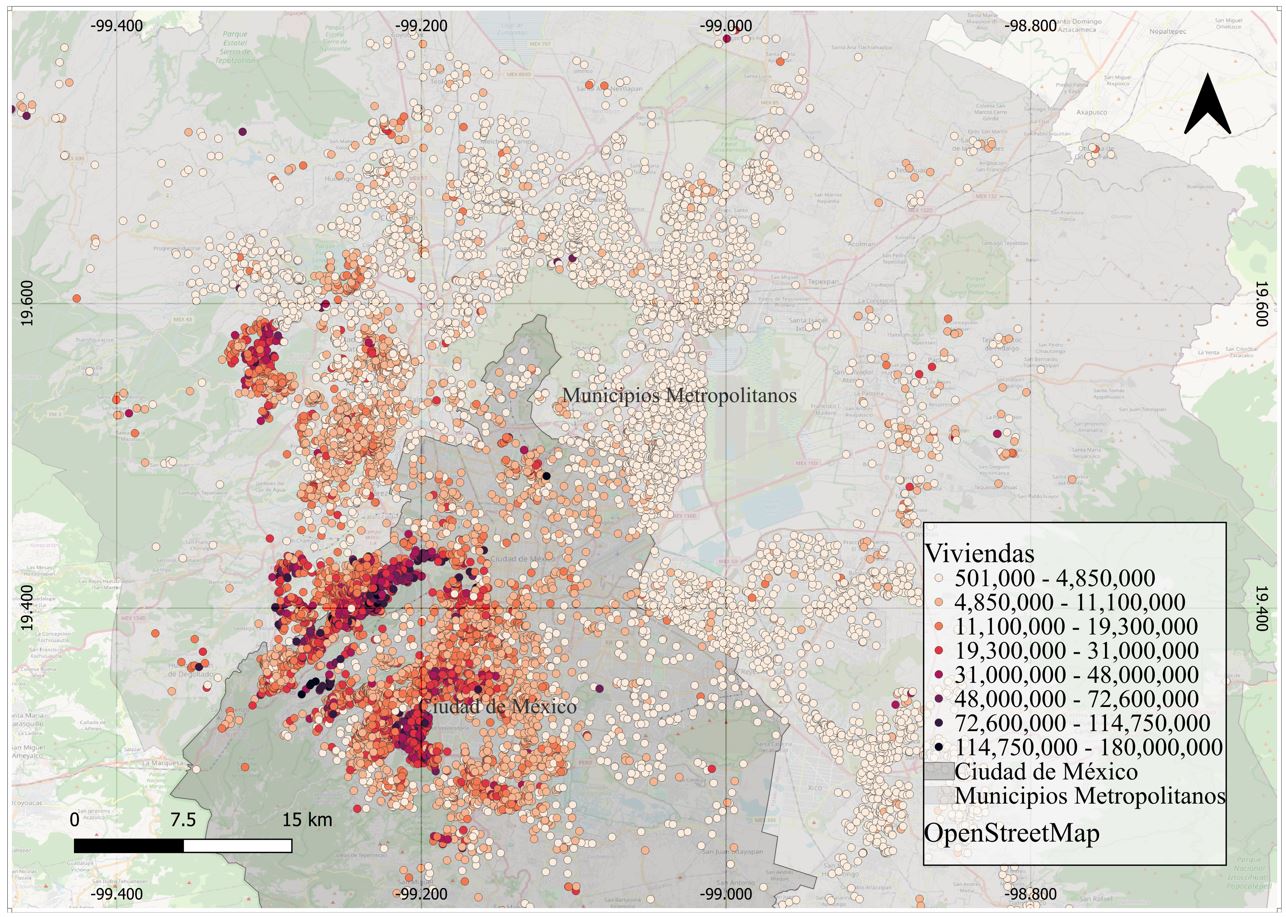 Mapa 7. Distribución espacial del precio
Mapa 7. Distribución espacial del precio
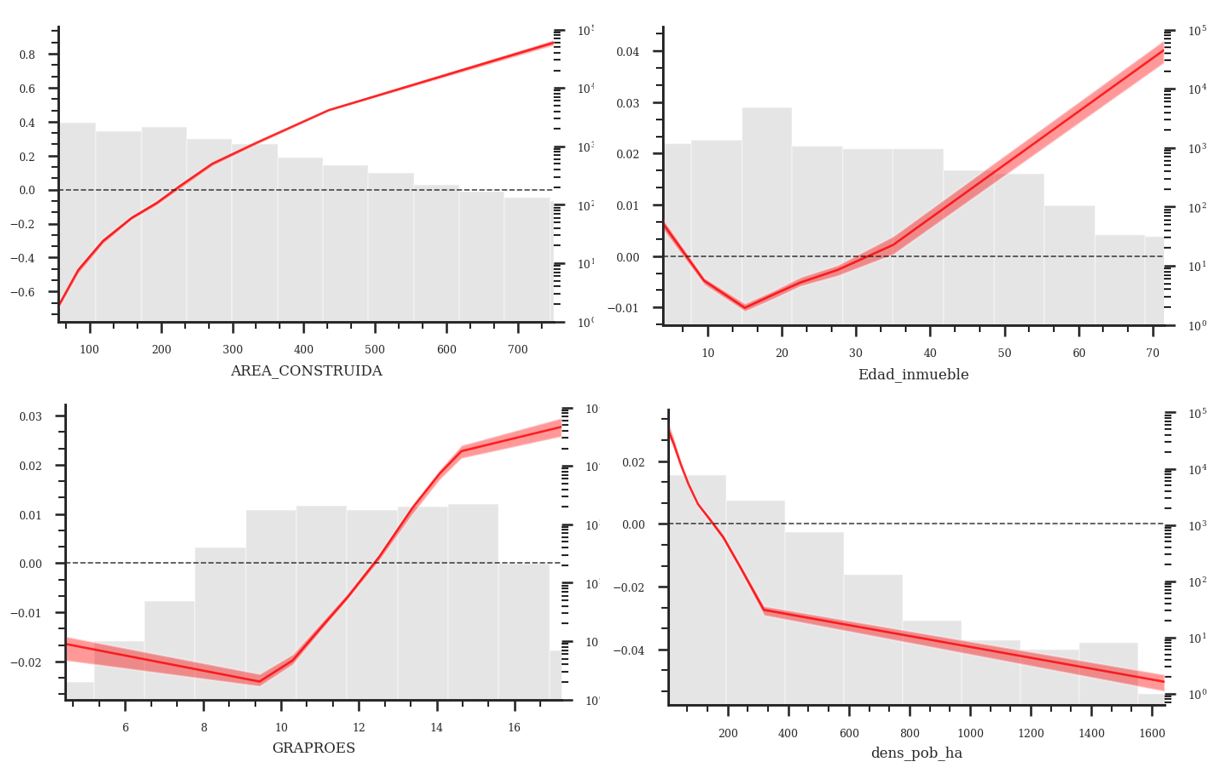 Gráfica 1. ALE, Área construida, Edad, Densidad, Escolaridad
Gráfica 1. ALE, Área construida, Edad, Densidad, Escolaridad
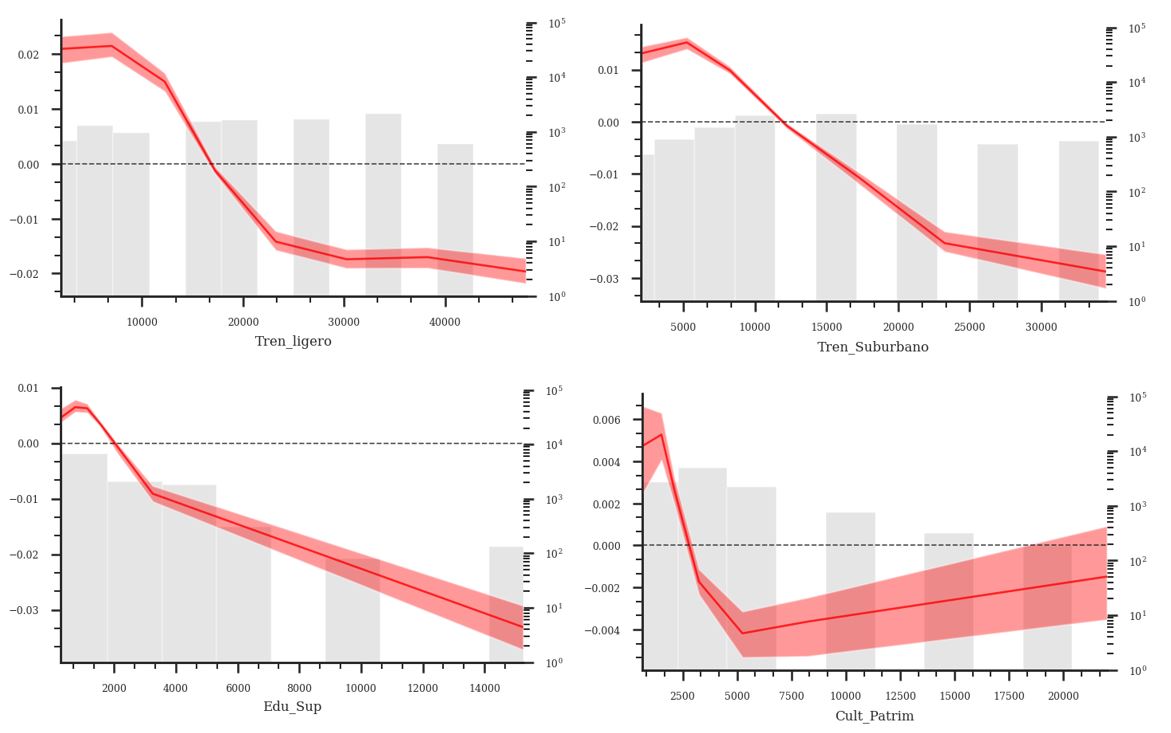 Gráfica 2. ALE, Tren Ligero, Tren Suburbano, Educación Superior, Cultura y Patrimonio
Gráfica 2. ALE, Tren Ligero, Tren Suburbano, Educación Superior, Cultura y Patrimonio
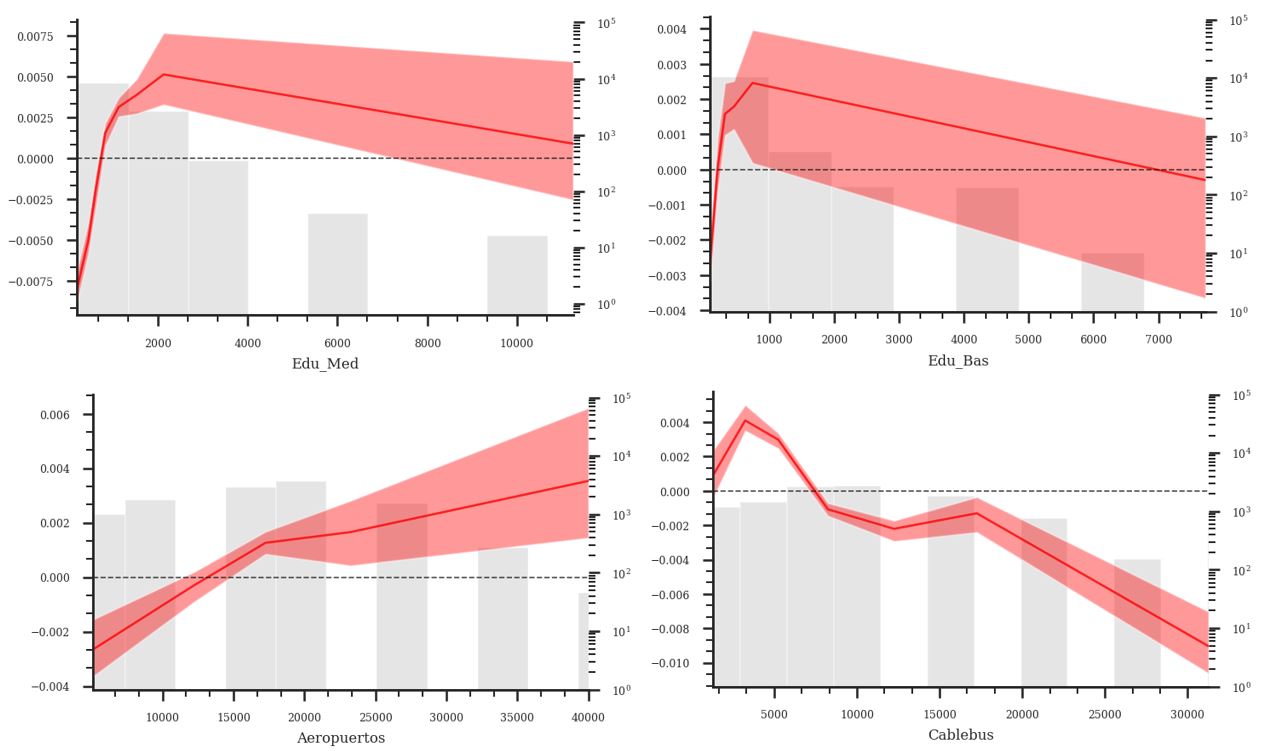 Gráfica 3. ALE, Educación basica, Educación media superior, Aeropuertos, Cablebus
Gráfica 3. ALE, Educación basica, Educación media superior, Aeropuertos, Cablebus
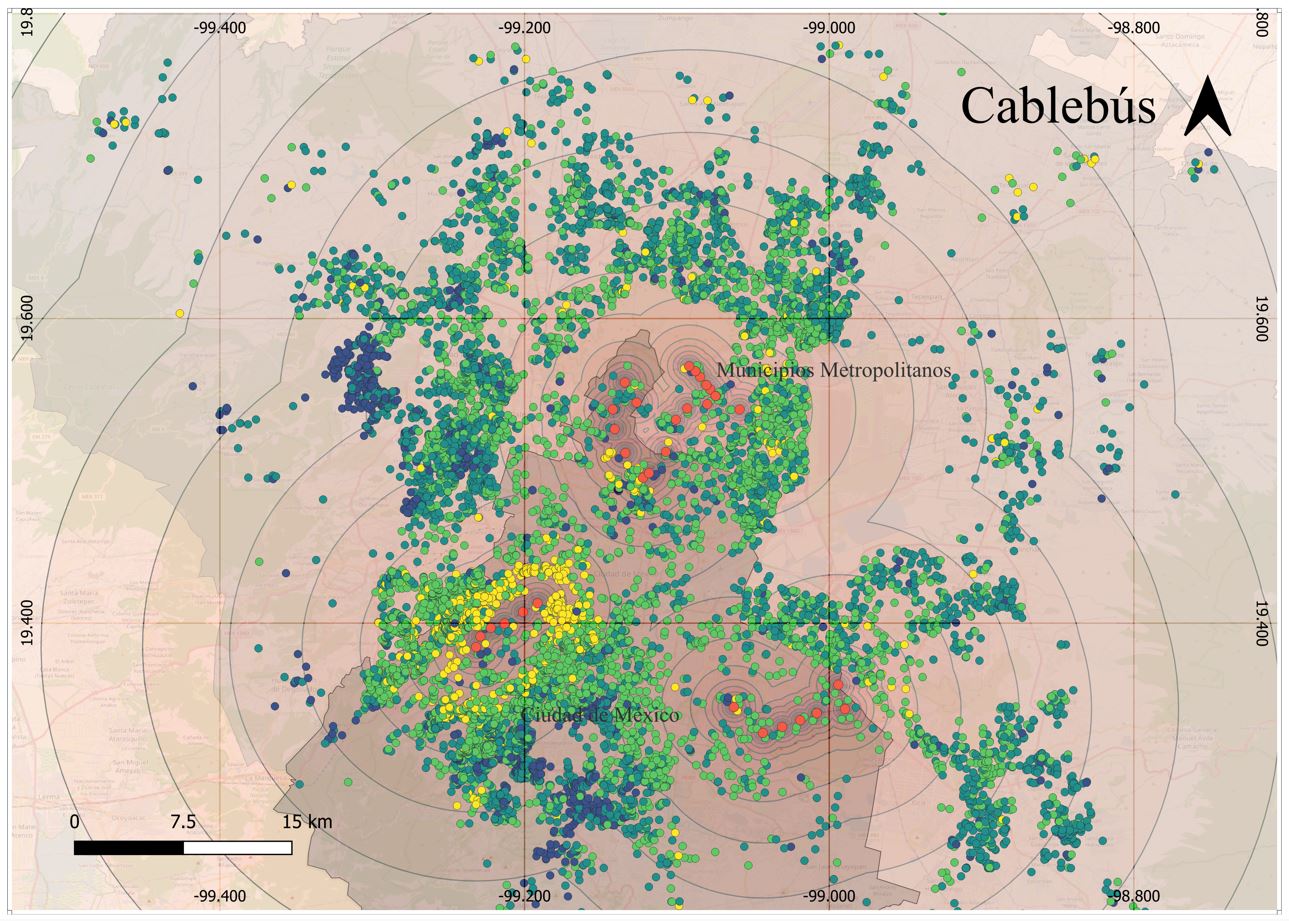 Mapa 8. SHAP, Cablebus
Mapa 8. SHAP, Cablebus
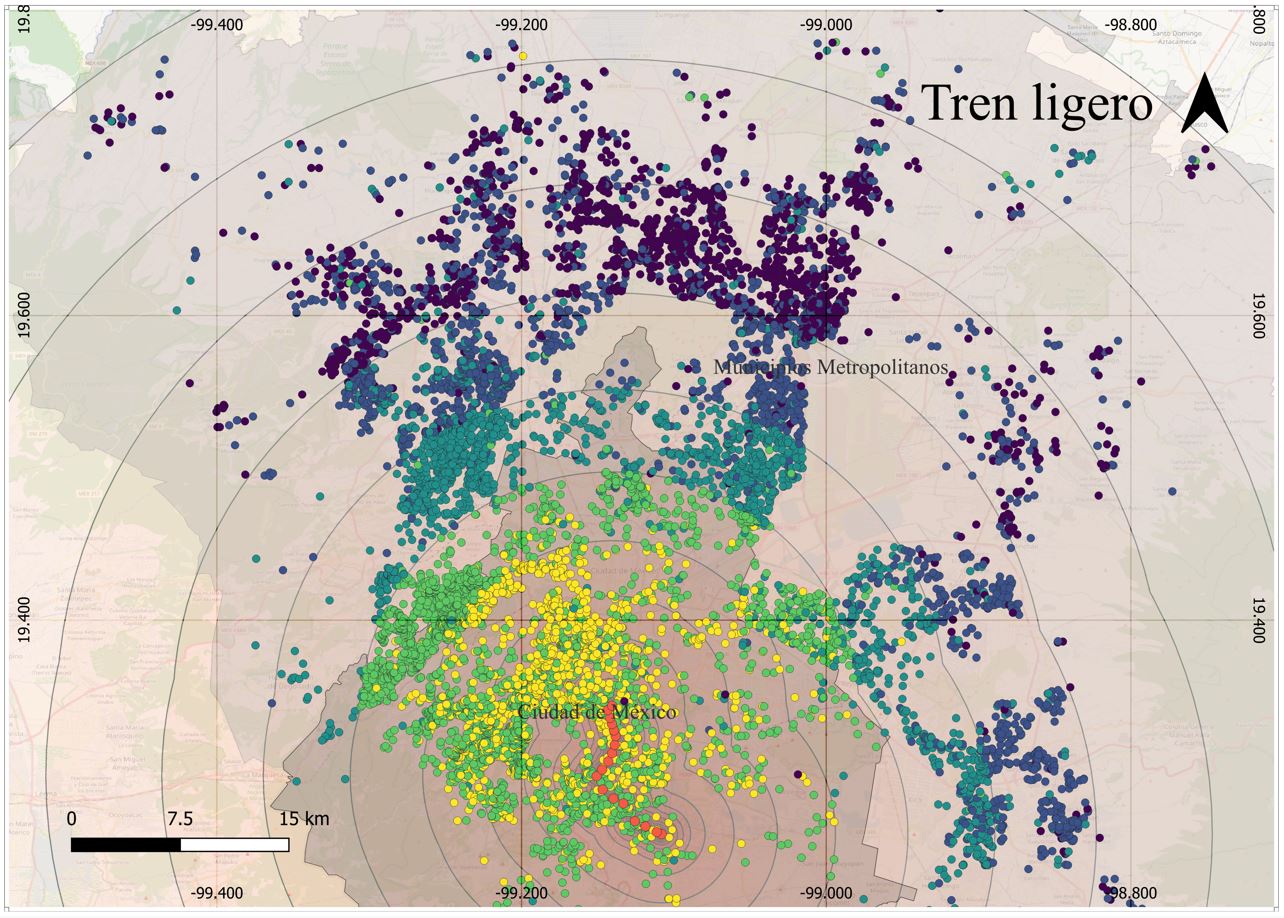 Mapa 9. SHAP, Tren ligero
Mapa 9. SHAP, Tren ligero
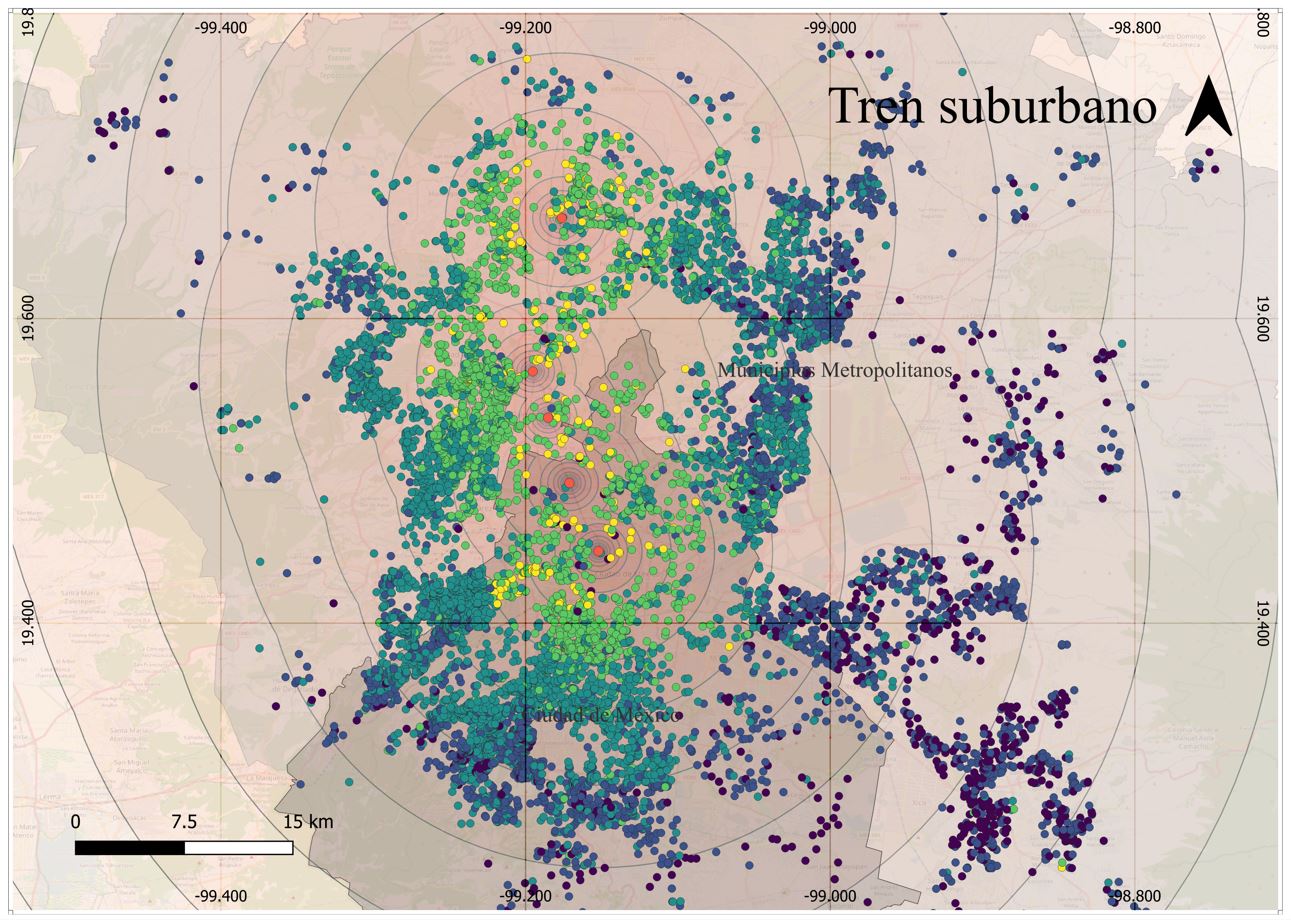 Mapa 10. SHAP, Tren Suburbano
Mapa 10. SHAP, Tren Suburbano
Politicas públicas
Desde una perspectiva fiscal, estos hallazgos respaldan la viabilidad de esquemas tributarios basados en la concentración territorial del valor, como el impuesto predial progresivo o los mecanismos de captura de plusvalías. A pesar de establecerse, en el articulo 115 constitucional, que el valor catastral debe equipararse al de mercado, la realidad del pais muestra, sin embargo, que existe un rezago de hasta el 50% en el valor en todo el territorio. Identificar espacialmente dónde se localiza el valor y cómo afecta al precio la cercanía a los distintos elementos urbanos permite justificar una mayor carga tributaria en aquellas zonas que concentran los mayores beneficios públicos. Este análisis podría mejorar el diseño y recaudación de diferentes instrumetos fiscales, incrementando los ingresos locales y favoreciendo su redistribución hacia otras zonas. Así, se contribuiría a reducir las brechas históricas de desigualdad que caracterizan a la metrópoli.

Consulta el estudio completo Aqui